Motivation

Most people when they were kids were fascinated by magicians and magic tricks, they were captivated by what appeared to be reality-defying and riddled with curiosity about how it was being done to the point they wished they become professional magicians as adults. Some of them took that fascination and curiosity to the next level and started to self-learn how to do magic tricks. But no matter how many tricks they knew, they didn’t really master the art of misdirection and the psychological aspects of manipulating the audience’s attention. Some took the extra mile and went to train under professional magicians, while the other continued with their mediocre skills. I was not part of either crowd; I tried doing magic tricks as a kid and I sucked at it! I was however drawn to some other kind of magic, the thing we call computer programming.

Programming indeed resembles magic. I guess the words of Guy Steele form Coders at Work are enough to capture this point:

I think it’s not an accident that we often use the imagery of magic to describe programming. We speak of computing wizards and we think of things happening by magic or automagically. And I think that’s because being able to get a machine to do what you want is the closest thing we’ve got in technology to adolescent wish-fulfillment.

And like magic, the phenomenon of self-learning prevailed in the computer programming world. The stackoverflow developers survey for the last two years showed that 41.8% of developers were self-taught in 2015 and 69.1% in 2016. I myself started, like many others, as a self-taught programmer before I went to college and studied computer science in depth.

The fact that I got to study computer science’s theory when my full-time job was to study was indeed a bliss. Attempting to study these subjects while you’re already involved in the industry can be quite a challenge, and I was lucky to be exempted from that.

The reason that it’s challenge to study the theory while already being out on the fields is that it complicates the binary work/life balance and transforms it into a ternary work/study/life balance! Being enrolled into a full program while you attempt to get your work done and keep your life going as straight as possible, provided that you remain sane throughout the whole process, is no doubt exhausting! However, the dauntingness of that balance is somehow mitigated these days thanks to the amazing work done by the people here on the Internet.

Nowadays we can find lots of videos, articles and blog posts as well as self-paced on-demand MOOC lectures on nearly every aspect of computer science. A lot of which are carefully written, beautifully explained and presented and freely accessible, and most of which can be covered in an hour or two each. The existence of these resources allows the self-learning process to be more comprehensive and makes the work/life/study balance more manageable. Unfortunately, this is not entirely true for the trending new kind of wizardry called machine learning.

Although I started to self-learn machine learning (ML) since my second year in college, only after my graduation I found myself in the phase of realizing that I’m missing a lot of foundations. So I practically found myself in the same situation I was happy I avoided before, but this time in the realm of ML theory where the monsters are not as tamed as the beasts of computer science world.

On the practical side of ML, the Internet is full of resources of the aforementioned kind through which I and many others self-learned. But on the theoretical side the case is not the same; you can find books, lecture notes, and even full lectures, but most of them do not offer the same flexibility you get form a series of blog posts, a series of short videos, or a MOOC where the collective effort of the students breaks the intimidation of the subject.

However, being equipped with my computer science study experience, and having some time flexibility in my current life phase; I embarked on the journey through the ML theory realm, and it’s been gratifying!

This series of posts is motivated by the desire to fill the gap in self-learnability between practical and theoretical ML, thus making the journey a little less daunting to embark.

Who is this Series for?

This series is intended to provide a gentle introduction to the theoretical aspects of machine learning, it would be beneficial to you if you’re :

If you’re a complete beginner in ML, this is probably not the best starting place for you. You you’d be better off by beginning with practical tutorials. After you get a hang of ML practice, you can come back here if you feel the need.

Prerequisites

A theory requires mathematics, and machine learning theory is no exception. But, as this is intended to be only a simple introduction, we will not be delving too deep into the mathematical analysis. We’ll focus more on the intuition of the theory with a sufficient amount of math to retain the rigor.

Most of the knowledge required on your part is: basics of probability and random variable, and calculus. As a person with some practical experience in ML, you should already have those.

As I’ll try to keep this series as self-containing as possible, I’ll attempt to go over any more advanced tools that we might need in our work.

Cautions

Now that we got the logistics of this work out of the way, we’ll conclude this part with a quick formalization of the ML problem in which we develop the mathematical entities and framework that we’ll use to investigate the theory in the upcoming parts.

Formalizing the Learning Problem

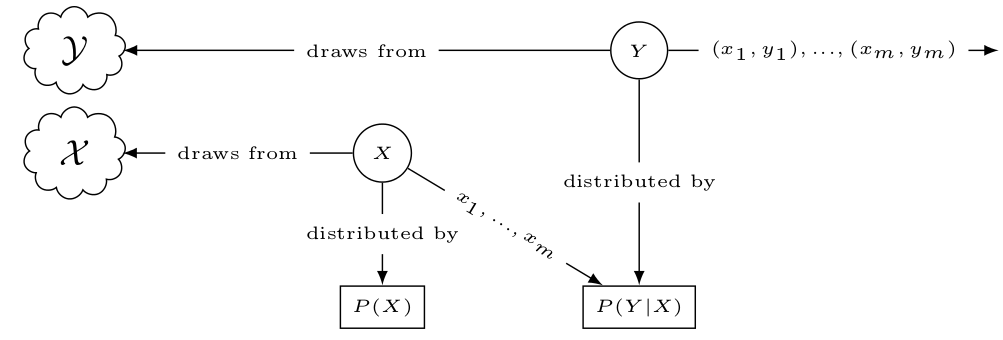
In this series we’ll focus primarily on the supervised learning problem, in which we have a dataset of observations $S = \{(x_1, y_1), …, (x_m, y_m)\}$ where $x_i$ is a feature vector and $y_i$ is a label and we which to learn how to infer the value of $y_i$ given $x_i$. For an example, $x_i$ can be a vector of specific medical measurements and tests results (such as blood glucose level, and body mass index) of a patient and $y_i$ is the whether that patient is diabetic, and we wish to learn how to diagnose diabetes given the set of medical tests results.

To start building our theoretical framework, it’s helpful to reiterate what we naively know about the situation at hand:

  1. We know that the values of $(x_i, y_i)$ in the dataset are just a random sample from a bigger population. In the concrete example we gave, the dataset is a random sample of a larger population of possible patients.
    • We can formalize this fact by saying that the values of $x_i$ and $y_i$ are realizations of two random variables $X$ and $Y$ with probability distributions $P_X$ and $P_Y$ respectively. Note that from now on, unless it’s pointed otherwise, we’ll refer to random variables with uppercase letters $X, Y,Z,…$ while we refer to the values that these varibles could take with lowercase letters $x,y,z,…$.
  2. We know that there are some rules on the values of $X$ and $Y$ that we expect any realization of them to follow. In the diabetes example, we know that a value of a blood glucose test (a component of the $x$ vector) cannot be negative, so it belongs to a space of positive numbers. We also know that value of the label can either be 0 (non-diabetic) or 1 (diabetic), so it belongs to a space containing only 0 and 1.
    • These kind of rules define what we formally call a space. We say that $X$ takes values drawn from the input space $\mathcal{X}$, and $Y$ from the output space $\mathcal{Y}$.
  3. We know that there is a relation between the features and the labels, in a sense that the value of the features somehow determines the value of the label, or that the value of $Y$ is conditioned on the value of $X$.
    • Formally, we express that by saying that there’s a conditional probability $P(Y|X)$. We can utilize this to compress the two distributions we had in the 1st point into a single joint distribution $P(X, Y) = P(X)P(Y|X)$.

With these three points, we can define a statistical model that formalizes everything we know about the learning problem. The following figure visually describes the model through process of generating the dataset $S$ sampled from the input and output spaces $\mathcal{X, Y}$ given the joint probability $P(X,Y)$.

Figure 1

The Target Function

It’s now clear from the statistical model we developed that the fundamental task of the machine learning process is to understand the nature of the conditional distribution $P(Y|X)$. To make our lives easier, we’ll avoid the hassle of working directly with the conditional distribution and instead introduce some kind of proxy that will be simpler to work with.

There are two fundamental statistics we can use to decompose a random variable: these are the mean (or the expected value) and the variance. The mean is the value around which the random variable is centered, and the variance is the measure of how the random variable is distributed around the mean. Given two random variables $V$ and $W$, we can say that:

\[V = \mathbb{E}[V|W] + (V - \mathbb{E}[V|W])\]

where $\mathbb{E}[V|W]$ is the conditional mean of the random variable $V$ given $W$. This essentially means that we can decompose the value of $V$ into two parts: the first can be explained in terms of the other variable $W$, and another noisy part that cannot be explained by $W$.

We can denote the unexplained part as an independent random variable $Z = V - \mathbb{E}[V|W]$. It easy to see (using the law of total expectation) that the mean of the $Z$ is zero. Hence $Z$ is a source of pure variance, that is the variance in V that cannot be explained by W.

Now we can write the relationship between any two associated realizations $(w_i, v_i)$ of $W$ and $V$ as:

\[v_i = \mathbb{E}[V|W=w_i] + \zeta\]

where $\zeta$ is a realization of the noise variable $Z$, we call that the noise term. We can apply the same reasoning on the our statistical model to get the following for any realization $(x_i, y_i)$.

\[y_i = \mathbb{E}[Y|X=x_i] + \zeta\]

Now It’s easy to notice that there is some function $f:\mathcal{X} \rightarrow \mathcal{Y}$ such that:

\[\mathbb{E}[Y|X=x] = f(x)\]

That is, the conditional expectation is a function of the realizations $x$ that maps the input space $\mathcal{X}$ to the output space $\mathcal{Y}$. Now we can describe the relation between the features and the labels using the formula:

\[y = f(x) + \zeta\]

Thus abstracting any mention of the conditional distribution $P(Y|X)$. Now we can use the function $f=f(x)$, which we call the target function, as the proxy for the conditional distribution. The statistical model now simplifies to the following.

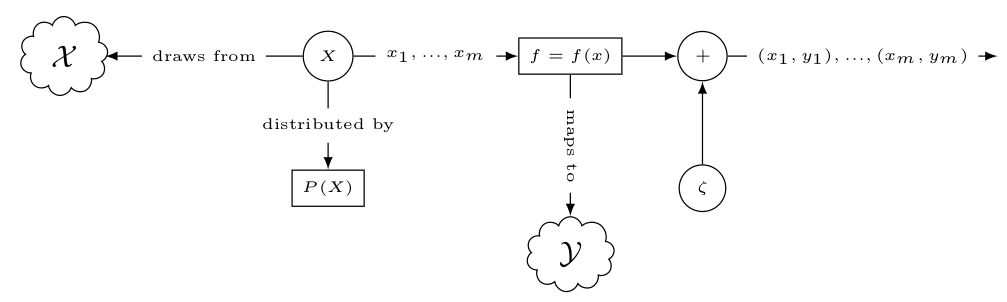
It’s called the target function because now it becomes the target of the machine learning process. The machine learning process is now simplified to the task of estimating the function $f$. We’ll later see how by this simplification we revealed the first source of error in our eventual solution.

The Hypothesis

In the process to estimate the target function from the sample dataset, because we cannot investigate every single function that could exist in the universe (there is an infinite kinds of them), we attempt to make a hypothesis about the form of $f$. We can hypothesize that $f$ is a linear function of the input, or a cubic one, or some sophisticated non-linear function represented by a neural network. Whatever a form we hypothesize about the the target function $f$, it defines a space of possible functions we call the hypothesis space $\mathcal{H}$.

If we hypothesize that the function $f$ takes the form $ax + b$, then we’re actually defining a hypothesis space $\mathcal{H}$ where:

\[\mathcal{H} = \{h:\mathcal{X} \rightarrow \mathcal{Y} | h(x) = ax + b\}\]

That is the set of all functions $h$ mapping the input space to the output space, taking the form $ax + b$. A function $h_1(x) = 3.2x - 1$ is a concrete instance of $\mathcal{H}$.

The task of the machine learning process now is to pick from $\mathcal{H}$ a single concrete function $h$ that best estimates the target function $f$. But how can measure how well a hypothesis function estimates the target? What is the criterion?

The Loss Function

One way of evaluating how well a hypothesis function is estimating the target function is by noticing that miss-labeling by the hypothesis should be discouraged, we obviously don’t want our hypothesis function to make too many mistakes! This is the role of the loss function $L=L(y,\hat{y})$ (also called the cost function).

The loss function takes the true label $y$ of some feature vector $x$, and the estimated label by our hypothesis $\hat{y}=h(x)$, then it examines how far our estimate is the from the true value and reports how much do we loose by using that hypothesis.

Using the loss function, we can calculate the performance of a hypothesis function $h$ on the entire dataset by taking the mean of the losses on each sample. We call this quantity the in-sample error, or as we’ll call it from now on: the empirical risk:

\[R_{\text{emp}}(h) = \frac{1}{m}\sum_{i=1}^{m}L(y_i, h(x_i))\]

It’s empirical because we calculate it form the empirical data we sampled in the dataset, but why don’t we call an empirical error? The reason behind that is notational; if we used the term error we’ll end up using $E$ to refer to it in the math, and this could lead into confusion with the notation for the expected value $\mathbb{E}$, hence we use risk and $R$ instead. The notational choice is also justified by the fact that error and risk are semantically close.

By defining the empirical error, the machine learning process can now chose the hypothesis with the last $R_{\text{emp}}(h)$ as the best estimation of the target function $f$. But is that it? Can we declare the problem solved?

The Generalization Error

What do you think of the following as a hypothesis? We memorize each sample in the dataset in a table, and whenever the the hypothesis function is queried with a feature vector $x_i$ we respond with associated $y_i$ in the table. Obviously, $R_{\text{emp}} = 0$ for this hypothesis. It’s also obvious that this is a lousy solution to the learning problem!

Remember that the goal is to learn the probability distribution underlying the dataset, not just do well on the dataset samples. That means that the hypothesis should also have low errors on new unseen data samples from the distribution. This is obviously not true for the proposed memorization hypothesis.

For the hypothesis to perform well on unseen new data is for the hypothesis to generalize over the underlying probability distribution. We formally capture that by defining the generalization error (also referred to as the risk), it simply the expected value of the loss over the whole joint distribution $P(X,Y)$:

\[R(h) = \mathbb{E}_{(x,y) \sim P(X,Y)}[L(y, h(x))]\]

Now we can say that the solution to the learning problem is the hypothesis with the least generalization error $R$. Simple, isn’t it? Well, here is the catch: we cannot calculate $R$ because we do not know the joint distribution $P(X,Y)$!

Is the Learning Problem Solvable?

Now that’s frustrating, we’re stuck our empirical risk minimization (ERM) strategy, is there even a chance that we can solve the learning problem?!

Well, we shouldn’t lose hope so fast. There is a chance to solve the learning problem if there’s a way that we can make both $R_{\text{emp}}(h)$ and $R(h)$ close to each other, but is that possible?

This question boils down to calculating the following probability:

\[\mathbb{P}[\sup_{h \in \mathcal{H}}|R(h) - R_{\text{emp}}(h)| > \epsilon]\]

That is the probability that the least upper bound (that is the supremum $\sup_{h \in \mathcal{H}}$) of the absolute difference between $R$ and $R_{\text{emp}}$ is larger than a very small value $\epsilon$. If this probability is sufficiently small, that is there is a very little chance that $R_{\text{emp}}$ differs much than $R$, then the learning problem is solvable.

This is the point of investigation in the next part of the series.

References and Additional Readings